Programming

Written in micropython, our codebase is devised of scheduler based tasks written as finite state machines with shared variables. Each peripheral has its own class with task class to handle its integration.

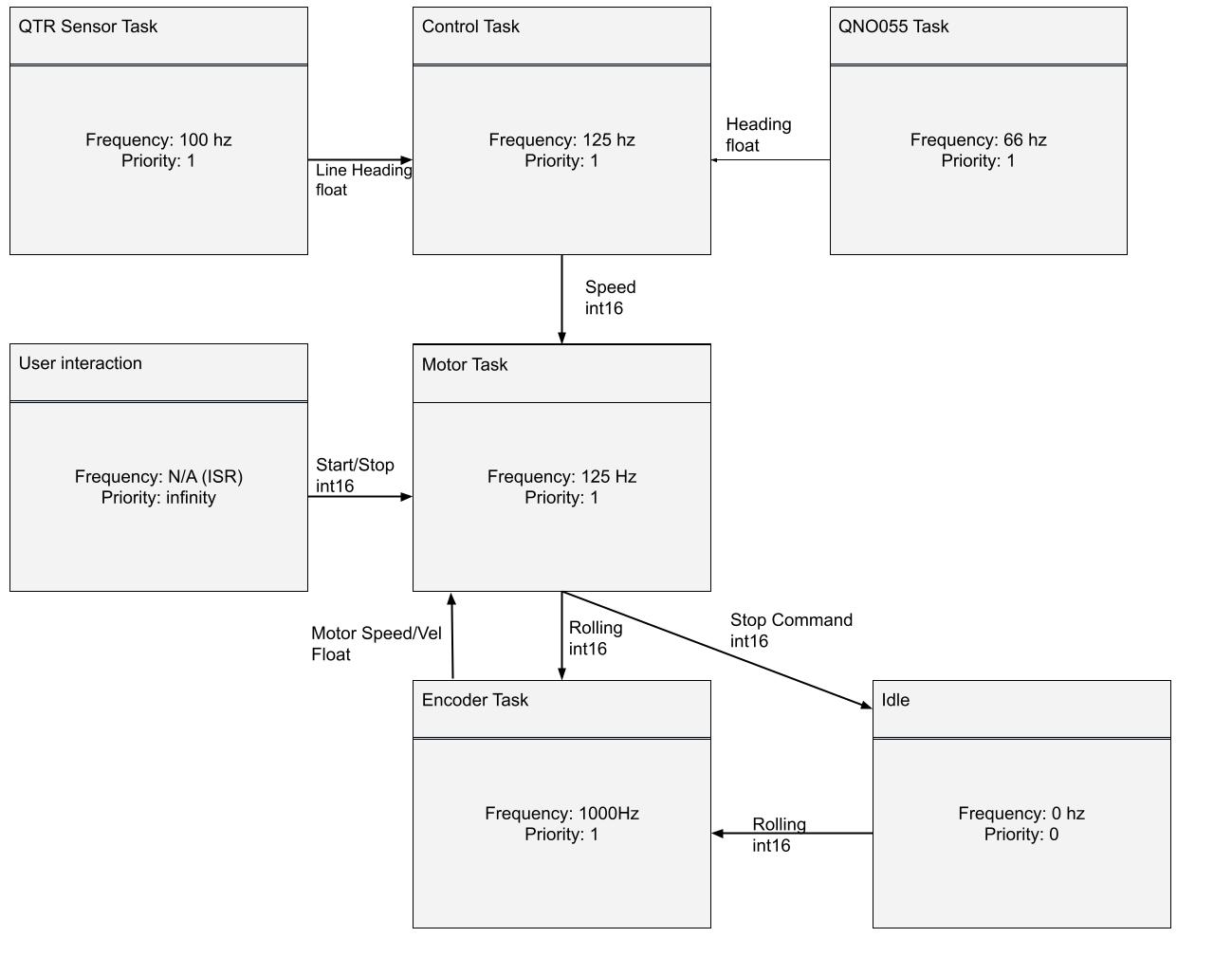
Tasks

We use Cal Poly’s ME405-Support libraries which provide the python files for implementation of tasks, shares and queues. This allows us to time when we get sensor readings, drive motors and use our controller. Shares allow us to have variables that different tasks can use and change. For example, our controller task can adjust the motor speed share which the motor task reads and uses to drive the motors to achieve a goal.

Shares

Shared Variable	Data Type	Purpose
right_pos	signed float	Encoder position in ticks of right motor
left_pos	signed float	Encoder position in ticks of left motor
right_vel	signed float	Velocity of right motor in ticks/us
left_vel	signed float	Velocity of left motor in ticks/us
right_speed	signed int	Desired direction and PWM % of right motor
left_speed	signed int	Desired direction and PWM % of left motor
right_stop	signed int	Value of stop state of right motor (0 on, 1 off)
left_stop	signed int	Value of stop state of left motor (0 on, 1 off)
line_error	signed float	Error value of black line under line sensor
heading	signed float	Current heading reading from IMU in degrees
heading_set	signed float	Desired heading angle in degrees
line_heading	signed int	Value determining controller state, (0, line following; 1 or -1 (reverse), heading following; 2, in place heading following (turn); 3, straight reverse; 4, stop)

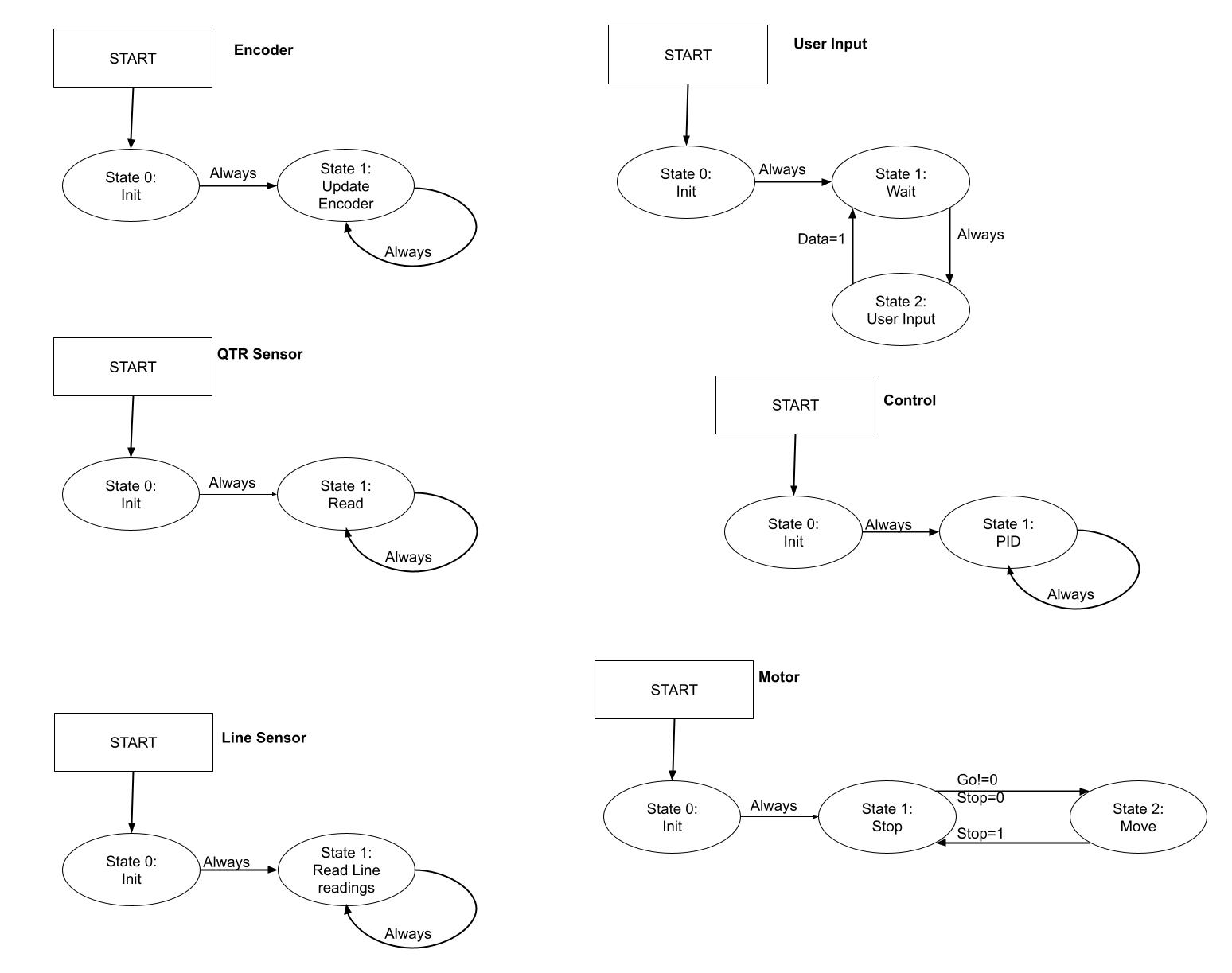
Finite State Machines

Each our tasks use generators written as finite state machines (FSM) Idk why but this FSM isnt updating from old jpg

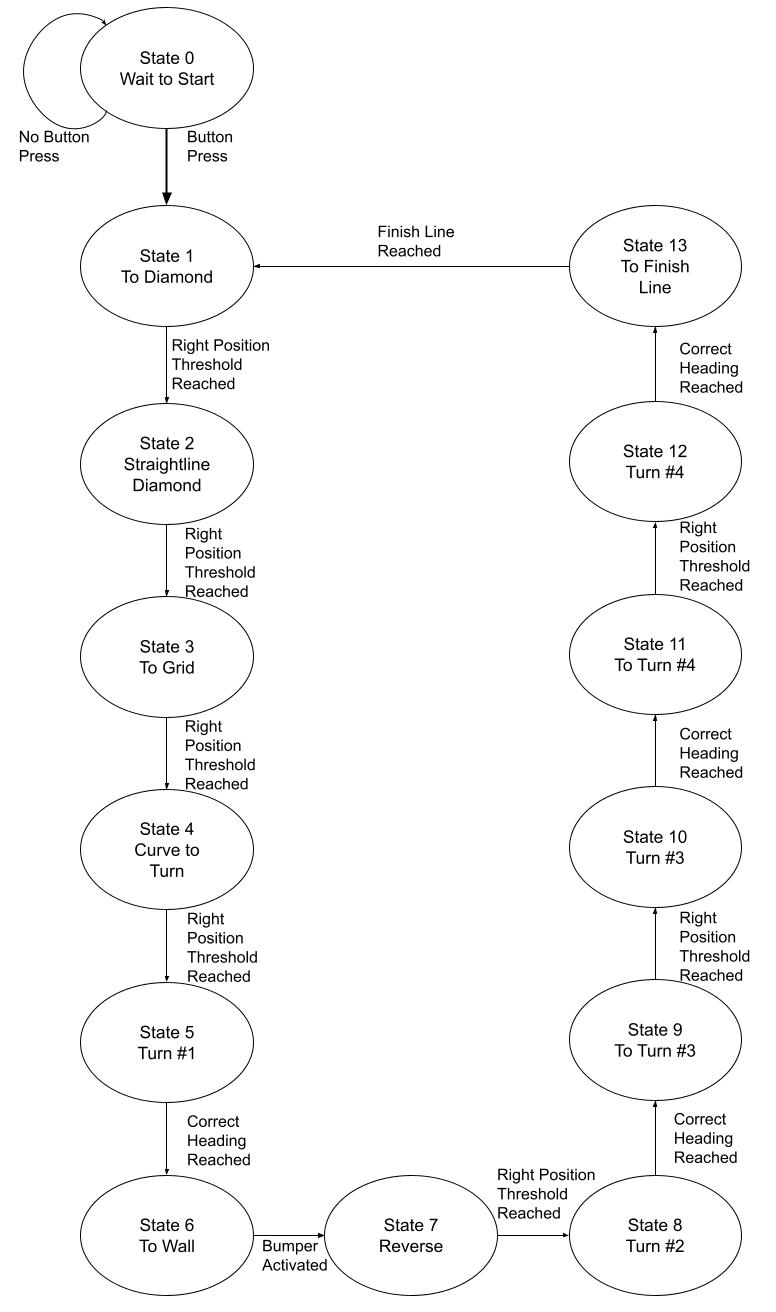
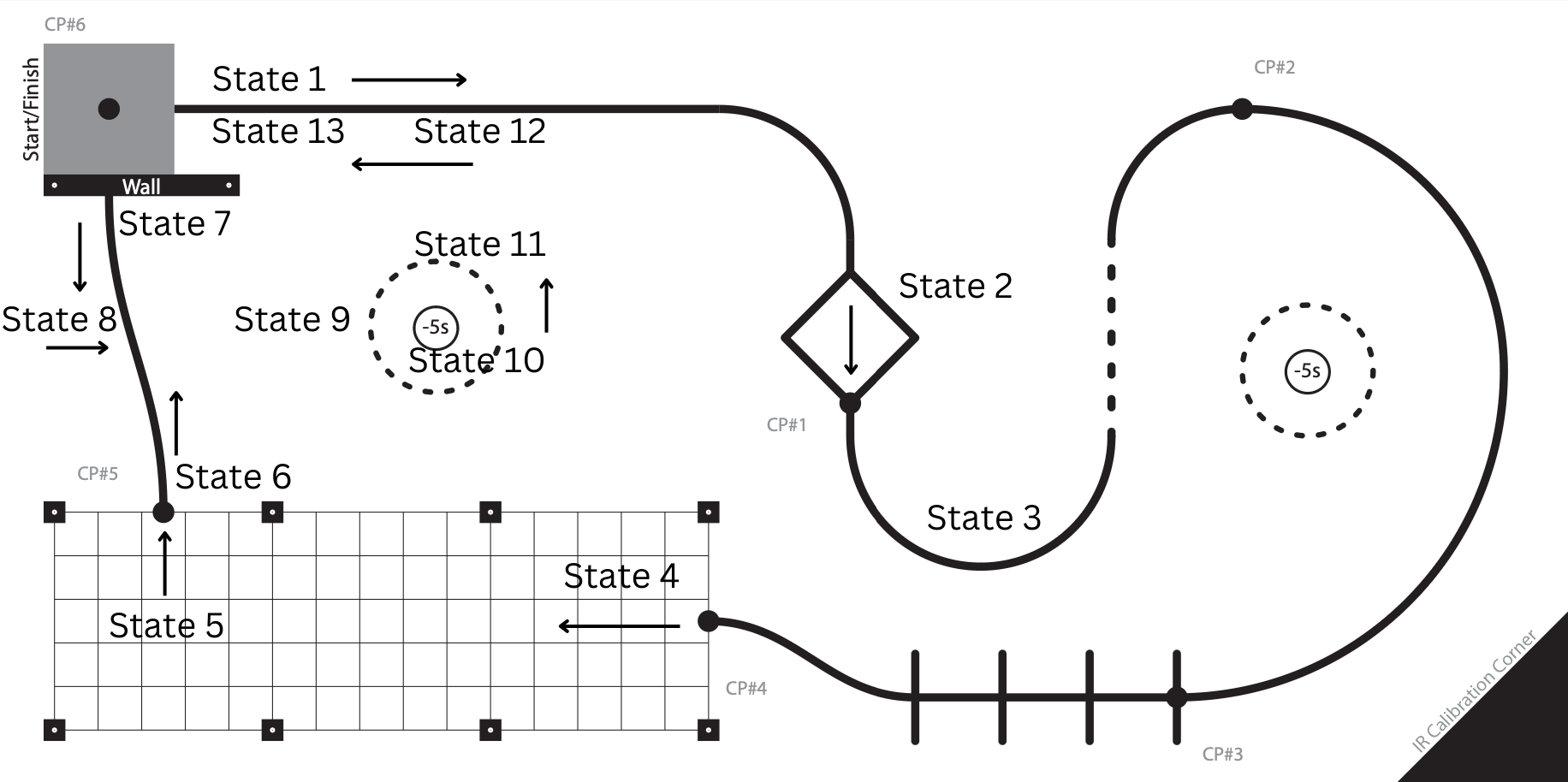
In main, we use a FSM to complete the course. It features hardcoded encoder position thresholds which jump between line following, heading following and full reverse modes.

Course FSM

Line Sensing Methods

Our line sensor features an array of light sensor that all produce a reading that can be normalized to 0 to 1 with a 1 being black. If the line is perfectly below the sensor, we get a ‘normal’ distribution with the middle sensors reporting a 1 while each sensor moving outwards has less black line under it. We use this theory to find the centroid of our sensor array which we can compare to the centroid of a perfectly centered line.

\[x = \frac{\sum_{i}q_i x_i}{\sum_{i}q_i}\]

where \(q_i\) is the sensor value and \(x_i\) is the sensor location

This is sent to our controller which tells the motors what to do to realign the robot with line.